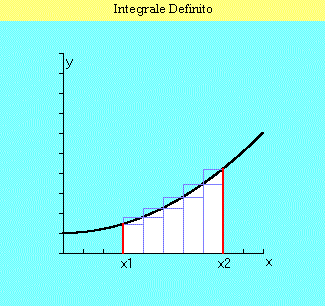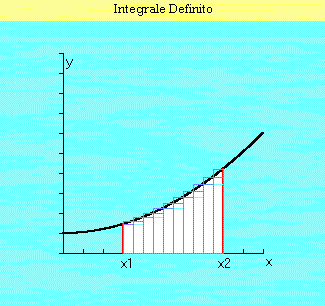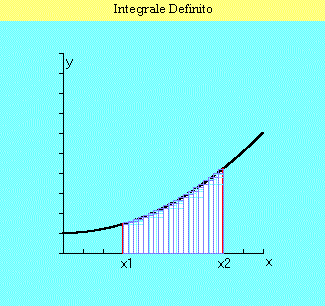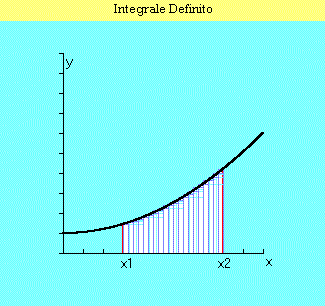
So,  if y(x) is a continuous and anywhere positive function in (x1-x2) interval and sn indicates the sum series of inscribed rectangles areas and Sn the similar one of circumscribed rectangles, it's possible to demonstrate that:
lim sn=	lim Sn
nое	nое
i.e. sn and  Sn are convergent series and they converge at the same number.
We can give then the definition of trapezoid area as the common limit of the above series. Remember that two series S1 and S2 of real numbers are convergent if they are contiguous, i.e.:
1-Any number of first series is less than any of the second one;
2-Arbitrarily fixing a positive small e.number, it's ever possible to find a s2 number of the second series and a s1 number of the first one so that:  s2-s1<e.