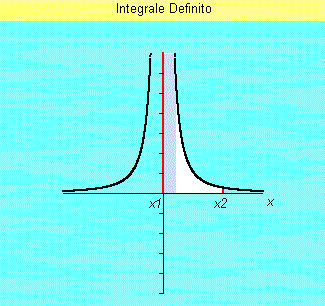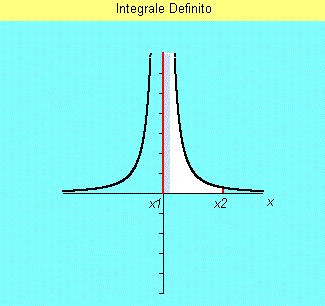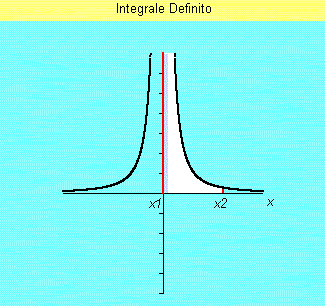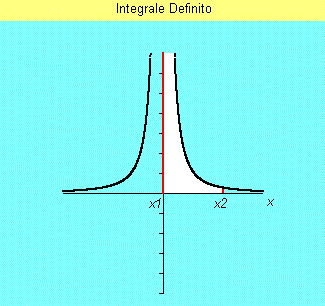
| We can then consider an integration interval (x1+e, x2) (corresponding to white zone), where e>0 is at will small a number, so we know how calcolate the integral: | ||||
| x2 | ||||
| ò y(x)dx | ||||
| x1+e | ||||
| because both in bound limits y(x) is now defined. If, vanishing e, this integral has a finite limit we can then put: | ||||
| x2 | x2 | |||
ò y(x)dx= |
lim | ò y(x)dx | ||
| x1 | e®0+ | x1+e | ||
| If otherwise this limit doesn't exist then the function is not integrable in (x1-x2) interval. | ||||